The unlikely nexus of The Skeptical Zone, Mung, noted the oddness, in the code that I provided in my last post, of using apparent constants not as constants, but instead as default values for parameters in functions. It was a reasonable remark, though what I was doing was not as odd as it seemed. There’s no denying that I should have explained myself in a comment. Looking things over, I decided to give non-programmers a shot at using the program by editing the values of those inconstant constants.
Two caveats. If Joe Felsenstein’s lovely post “Wright, Fisher, and the Weasel” makes little sense to you, running my program is unlikely to help. If you read ahead in this post, and feel that it’s too much for you, then it is. Give up. Honestly, it’s not worth the bother. If you remain interested, peruse the comments on Joe’s post, and ask questions of your own.
On with the instructions. First make sure that you have Python installed. The easiest approach I know is to open a command shell, and enter
at the prompt (which usually is something other than a dollar sign). On my Unix-like system, that puts me in the Python interpreter. It’s no place for non-programmers to be. To get out, enter$ python
(Your Python prompt will not necessarily be three greater-than signs.)>>> quit()
Now copy-and-paste the code from the big, black box below to a plain text file. (Your best bet is to use a simple text editor, not a word-processing application like MS Word.) Here’s your first taste of non-programming: go to the line
N_GENERATIONS=100000 # Number of generationsand delete one of the 0’s from the number. You’ll end up with this:
N_GENERATIONS=10000 # Number of generationsThis reduces the running time of the program by a factor of 10, which is a pretty good idea when you’re trying to determine whether it works. The leftward shift in the hash sign (#) is fine. In fact, it serves as a reminder that you changed something. You can extend the comment (text following # is ignored when the program runs) with a note to yourself.
N_GENERATIONS=10000 # Number of generations WAS 100000Now save the modified file. A
.PY extension would be a good idea. I’ll assume that you went with the name evolve.py.
If you submit the file to Python from a command prompt, with an incantation like
then the program will execute with parameter settings defined at the top of the file. You should see textual output similar to this in the command interpreter window.$ python < evolve.py
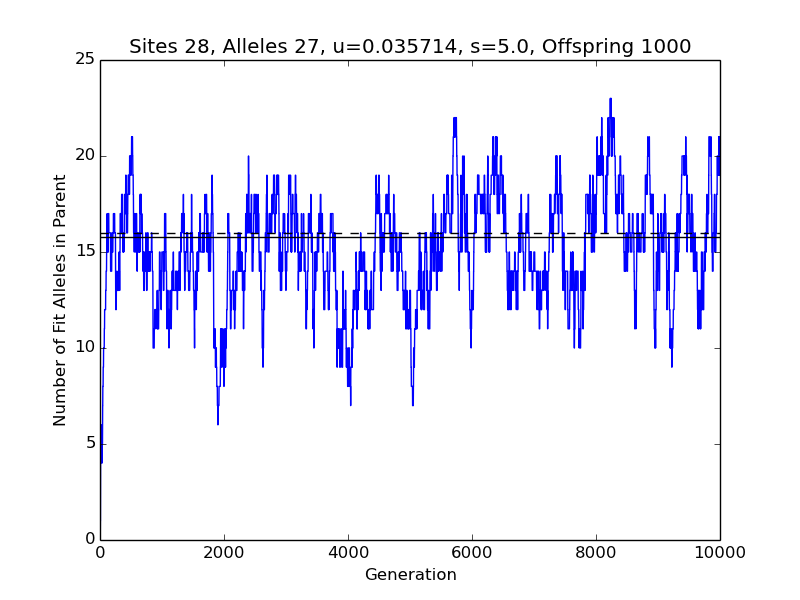
If you get an error message instead, and you’re not interested in Python programming, then give up. There are two main sources of problems. With an outdated version of the Numeric Python (************************************************************************ Number of sites L : 28 Number of possible alleles A : 27 Number of offspring : 1000 Mutation rate u : 0.0357142857143 Selection parameter s : 5.0 p = u * (1 + s) / (A-1 + u * s) : 0.00818553888131 q = u / (1 + s * (1 - u)) : 0.00613496932515 Assume equilibrium at generation: 5000 W-F probability of fit allele at site p/(p+q) : 0.571595558153 Expected num. of fit alleles in parent Lp/(p+q): 16.0046756283 Mean observed num. of fit alleles in parent : 15.7896420716 Std. dev. of observed numbers of fit alleles : 2.78893977254 ************************************************************************
numpy) module, you might see an error message ending with
or withAttributeError: 'module' object has no attribute 'choice'
Another possibility is that your Python is not configured to do graphics. I cannot help you with either problem. But, if you’re willing to Google for instructions, you can fix them. What I hope is that you’ll see a graphical display pop open, looking something like this. If the display does not appear, check to see if it’s hidden behind other windows. No joy? Then there’s one last thing to try. EnterValueError: n <= 0
The$ python -i evolve.py
-i stands for interactive, which is to say, you’re about to land back where non-programmers do not belong. But you’ve seen already what is most import to know — how to make the blasted thing quit(). Then again, it wouldn’t hurt simply to double-click the icon for the file evolve.py. If you’ve gotten this far, don’t give up. You can Google for instructions on how to configure the Python graphics backend. It might help to add the name of your operating system to the search term. If you learn something that stands to help other folks, please take a moment to post a comment here.
Your squiggly line will squiggle differently than mine, because there's randomness (or unpredictability that passes for randomness) involved. The solid line is the average value of the plotted quantity over the last 5000 generations. The dotted line is the prediction of the Wright-Fisher model, which does not apply strictly to the program. Much of the discrepancy is due, probably, to the shortness of the run. If you had not reduced N_GENERATIONS by a factor of 10, the solid line would have indicated the average of observations for 95 thousand generations, and probably would have been closer to the dotted line. The more generations in the run, the less variable the mean value of the observations (which determines the placement of the solid line).
Now, the point of all of this is to see how changing the parameters changes the behavior of the evolutionary process. You can learn quite a bit by repeatedly (1) editing the values of the inconstant constants (at the top of the file, with all-caps names), (2) saving the change, and (3) submitting the revised file to Python. And why do you have to do it this way? Because I have not learned how to do graphical user interfaces in Python. It doesn’t seem to be a priority at the moment. Then again, if I were any good at prioritizing, you wouldn’t have gotten this much out of me.
import numpy as np import numpy.random as rand import matplotlib.pyplot as plt # Implement a model that is somewhat like Wright-Fisher, with Dawkins's Weasel # as a special case. # See Felsenstein (2016), "Wright, Fisher, and the Weasel," The Skeptical # Zone, http://theskepticalzone.com/wp/wright-fisher-and-the-weasel/. # # Copyright Tom English, 2016. # Permission for personal use granted. You may not redistribute this code, # irrespective of whether you have modified or augmented it. # The following are default values of model parameters. # You can use a text editor to change the values between runs of the program. # The all-caps notation tells programmers to change the values ONLY by editing. # N_SITES=28 # "Sentence length" (at least 1) N_ALLELES=27 # "Alphabet size" (at least 2) MUTATE_RATE=1.0/N_SITES # Denoted u by Felsenstein (0.0 < u < 1.0) N_OFFSPRING=1000 # Number of offspring per generation (at least 1) SELECTION=5.0 # Denoted s by Felsenstein N_GENERATIONS=100000 # Number of generations EQUILIBRIUM_BEGIN=5000 # Evolution assumed stable after this many generations assert(N_SITES >= 1) assert(N_ALLELES >= 2) assert(MUTATE_RATE > 0.0 and MUTATE_RATE < 1.0) assert(N_OFFSPRING >= 1) class Evolve(object): """ Model somewhat like Wright-Fisher, with Dawkins's Weasel as a special case. """ def __init__(self, n_sites=int(N_SITES), n_alleles=int(N_ALLELES), n_offspring=int(N_OFFSPRING), mutate_rate=MUTATE_RATE, selection=float(SELECTION)): """ Initialize evolutionary run. """ self.n_sites = n_sites self.n_alleles = n_alleles self.n_offspring = n_offspring self.mutate_rate = mutate_rate self.selection = selection self.probability = np.empty(n_offspring, dtype=float) self.offspring = np.empty(n_offspring, dtype=int) self.n_fit = rand.binomial(N_SITES, 1.0 / n_alleles) self.history = [self.n_fit] def generation(self): """ Extend evolutionary run by one generation. At each site, the allele is either fit or unfit. The probability of selecting an offspring as parent of the next generation is proportional to its fitness `(1+selection)**n_fit`, where `n_fit` is the number of fit alleles. """ n = len(self.offspring) loss_rate = self.mutate_rate gain_rate = self.mutate_rate / (self.n_alleles - 1.0) self.offspring[:] = self.n_fit self.offspring += rand.binomial(self.n_sites - self.n_fit, gain_rate, n) self.offspring -= rand.binomial(self.n_fit, loss_rate, n) np.power(self.selection + 1.0, self.offspring, self.probability) self.probability /= np.sum(self.probability) self.n_fit = rand.choice(self.offspring, size=1, p=self.probability) self.history.append(self.n_fit) def extend(self, n_generations=N_GENERATIONS): """ Extend evolutionary run by `n_generations` generations. """ for _ in xrange(n_generations): self.generation() def get_history(self, begin=0, end=None): """ Return list of nums. of fit alleles in parents for range of generations. """ return self.history[begin:end] def report(self, begin=EQUILIBRIUM_BEGIN): """ Report on some quantities addressed by Felsenstein (2016). """ u = self.mutate_rate s = self.selection q = u / (1 + s * (1 - u)) p = u * (1 + s) / (self.n_alleles - 1 + u * s) h = self.history[begin:] print '*'*72 print 'Number of sites L :', N_SITES print 'Number of possible alleles A :', self.n_alleles print 'Number of offspring :', len(self.offspring) print 'Mutation rate u :', u print 'Selection parameter s :', s print 'p = u * (1 + s) / (A-1 + u * s) :', p print 'q = u / (1 + s * (1 - u)) :', q print 'Assume equilibrium at generation:', begin print 'W-F probability of fit allele at site p/(p+q) :', p/(p+q) print 'Expected num. of fit alleles in parent Lp/(p+q):', N_SITES*p/(p+q) print 'Mean observed num. of fit alleles in parent :', np.mean(h) print 'Std. dev. of observed numbers of fit alleles :', np.std(h) print '*'*72 plt.plot(self.history) m = np.mean(h) plt.plot((0, len(self.history)-1), (m, m), 'k-') m = N_SITES * p/(p+q) plt.plot((0, len(self.history)-1), (m, m), 'k--') plt.ylabel('Number of Fit Alleles in Parent') plt.xlabel('Generation') plt.title('Sites {0}, Alleles {1}, u={2:.6f}, s={3}, Offspring {4}'. \ format(self.n_sites, self.n_alleles, self.mutate_rate, self.selection, self.n_offspring)) plt.show() def example(): """ Plot numbers of fit alleles for runs varying in just one parameter. """ plt.figure() n_generations = 100000 # Override the default N_GENERATIONS here equilibrium_begin = 5000 # Override the default EQUILIBRIUM_BEGIN here results = [] for s in [0, 2, 5, 15]: # Put other numbers in this list... e = Evolve(selection=s) # ... change `selection` to another parameter e.extend(n_generations) print 'Selection parameter s:', s e.report(begin=equilibrium_begin) results.append(e) plt.title('Weasel-ish Runs with Selection Parameter s in {0, 2, 5, 15}') plt.show() return results # Run with default parameter settings plt.figure() e=Evolve() e.extend() e.report() plt.show() # To run my example, intended primarily for programmers: # results=example() # Use plt.close('all') to close plots when interacting with Python.